扩散模型
扩散模型是一种特殊的VAE,其灵感来自于热力学:一个分布可以通过不断地添加噪声变成另一个分布。放到图像生成任务里,就是来自训练集的图像可以通过不断添加噪声变成符合标准正态分布的图像。 图像生成网络会学习如何把一个向量映射成一幅图像。设计网络架构时,最重要的是设计学习目标,让网络生成的图像和给定数据集里的图像相似。VAE的做法是使用两个网络,一个学习把图像编码成向量,另一个学习把向量解码回图像,它们的目标是让复原图像和原图像尽可能相似。学习完毕后,解码器就是图像生成网络。扩散模型是一种更具体的VAE。它把编码过程固定为加噪声,并让解码器学习怎么样消除之前添加的每一步噪声。
无标题
原型=动态演化的语义锚点 原型的关键作用 1. 类级表示 经过层级学习、去噪后的特征,更纯净、更有代表性 2. 对比学习的监督信号 不只是"拉近同类",而是"拉向类中心" 语义信息: 原型包含了这个类的核心特征 例如:猫原型 = “有毛” + “四条腿” + “小体型” 辅助分类: 新样本可以和各类原型对比 与哪个原型最接近,就属于哪一类 知识迁移: 原型可以在不同任务间共享
开学三个月小记
...
深度学习优化器全家桶:从 SGD 到 AdamW 及未来
在深度学习的训练过程中,优化器 (Optimizer) 扮演着至关重要的角色。它决定了网络参数更新的方式,直接影响模型的收敛速度和最终性能。本文将深入剖析深度学习中常见的优化器,从最基础的 SGD 到目前最流行的 AdamW,以及一些前沿的变体。 1. 梯度下降家族 (Gradient Descent Variants) 1.1 BGD, SGD 与 Mini-batch SGD BGD (Batch Gradient Descent):每次迭代使用全部样本计算梯度。 优点:梯度准确,收敛稳定。 缺点:计算量大,内存无法承受,无法在线更新。 SGD (Stochastic Gradient Descent):每次迭代使用一个样本。 优点:计算快,引入噪声有助于跳出局部最优。 缺点:震荡剧烈,收敛慢,无法利用向量化加速。 Mini-batch SGD:折中方案,每次使用一批样本(如 32, 64)。这是实际中最常用的形式。 $$ w_{t+1} = w_t - \eta \cdot \nabla L(w_t) $$ 1.2 Momentum (动量法) 为了抑制...
深度学习损失函数:从 MSE 到 Focal Loss
在深度学习中,损失函数 (Loss Function) 是连接模型预测与真实标签的桥梁,它定义了模型的优化目标。选择合适的损失函数往往能起到事半功倍的效果。本文将对深度学习中常见的损失函数进行梳理,从基础的回归/分类到进阶的难例挖掘和度量学习。 1. 回归任务 (Regression) 回归任务的目标是预测连续值。 1.1 MSE (L2 Loss) 均方误差 (Mean Squared Error): $$ L = (y - \hat{y})^2 $$ 特点:收敛快,但对异常值 (Outliers) 非常敏感(因为误差被平方放大了)。 1.2 MAE (L1 Loss) 平均绝对误差 (Mean Absolute Error): $$ L = |y - \hat{y}| $$ 特点:对异常值鲁棒,但在 0 点处不可导,梯度恒定可能导致收敛困难。 1.3 Smooth L1 Loss 结合了 L1 和 L2 的优点: 在误差较小时($|x| < 1$)使用 L2(平滑,可导)。 在误差较大时($|x| \ge 1$)使用...
深度学习杂谈:残差、MAE与特征维度的本质思考
最近有一些问题,正好记录下来了一些,用AI探讨了一下这些问题。 1. 残差 (Residual) 的本质:仅仅是保留原始信息吗? 问题: 残差的本质是什么?为什么有用?是因为保留了之前的原始信息的特征吗?那么添加动量 (Momentum) 也是保留之前的原始信息,和残差的本质有什么区别吗? 残差连接 (Skip Connection) 残差网络 (ResNet) 的核心公式是 $y = F(x) + x$。 确实,从直观上看,$+x$ 这一项直接将上一层的原始信息“保留”并传递到了下一层。这使得网络在初始化阶段即使 $F(x)$ 接近于 0,整个网络也近似于一个恒等映射 (Identity Mapping),梯度可以无损地反向传播。 本质区别: 残差 (ResNet) 解决的是 模型结构 (Model Architecture) 和 梯度流 (Gradient Flow) 的问题。它是在空间/层级维度上,让深层网络更容易训练,避免梯度消失。它让网络“有机会”去学习恒等映射,如果某一层是多余的,网络可以将 $F(x)$ 权重置为 0,自动“跳过”这一层。 动量...
监督对比学习
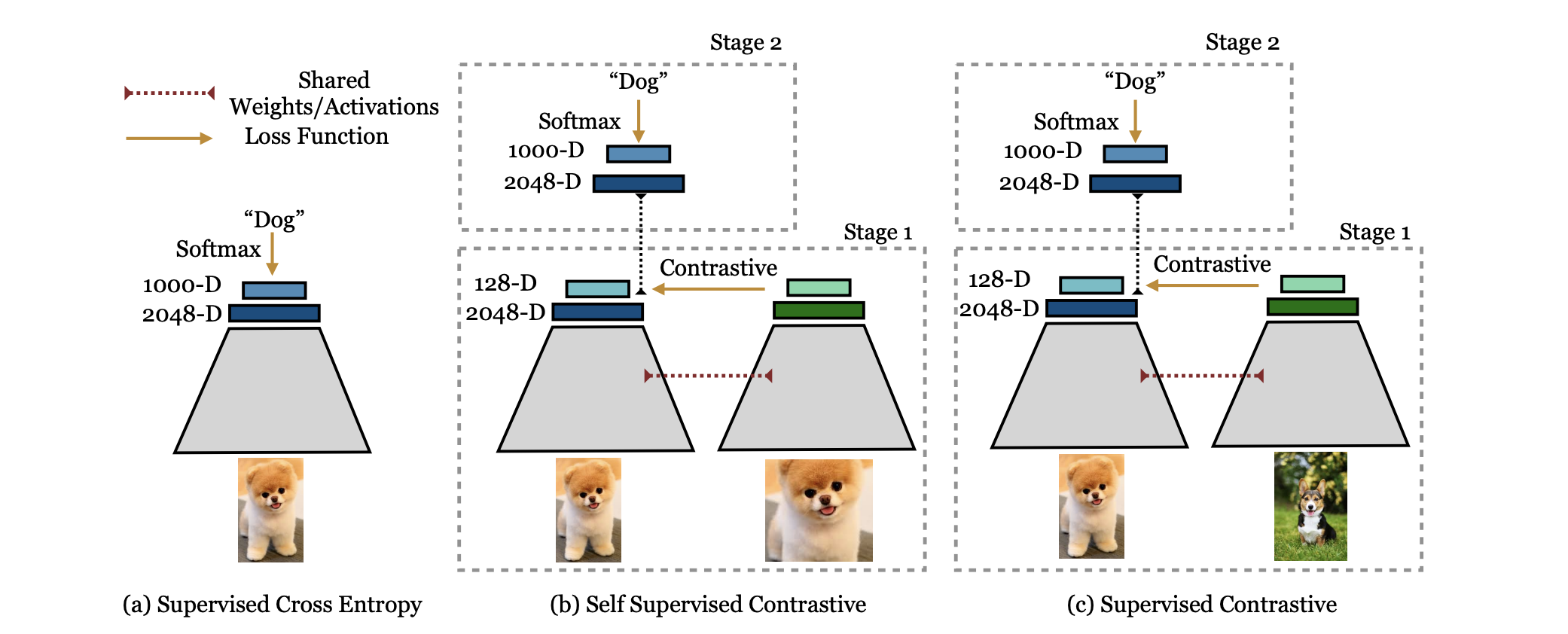
Supervised Contrastive Learning 论文地址:https://arxiv.org/pdf/2004.11362 代码地址:https://github.com/HobbitLong/SupContrast 引言 监督对比学习(Supervised Contrastive Learning, SupCon)...
对比学习综述
对比学习综述:从理论到实践全面解析 引言 对比学习(Contrastive Learning) 是近年来自监督学习领域最重要的突破之一,它通过"拉近正样本、推远负样本"的简单思想,在无需大量标注数据的情况下学习到强大的视觉表示。从2020年的SimCLR、MoCo开始,对比学习在ImageNet等基准上取得了与监督学习相当甚至更好的性能,彻底改变了我们对无监督表示学习的认知。 对比学习的核心优势在于: 无需标注数据:可以在海量无标注图像上预训练 学习鲁棒表示:对数据增强、噪声等具有强鲁棒性 迁移能力强:预训练的特征在下游任务上表现优异 可扩展性好:可以轻松扩展到大规模数据和模型 什么是对比学习? 核心思想 对比学习的核心思想可以用一句话概括:通过对比正样本对和负样本对,学习到区分性的表示。 正样本对(Positive Pairs):应该相似的样本对 无监督:同一图像的不同增强视图 有监督:同一类别的不同样本 负样本对(Negative...
LeetCode 两个变量 - 2025.11.13
今日概览 日期:{2025-11-13} 题目数量:{共 2 题} 难度分布:简单 2 主要收获:自己的方法就是屎山,灵神的方法高端又通透 心情/状态:太久没刷了,已经把基本的语法忘记了,以后尝试用python刷题,学习一些比较好用的函数 题目列表与详解 1. Two Sum 题号 / 链接:#1 / 题目链接 难度:简单 题型标签:哈希表,数组 题目描述(简要): 就是查找一下哪两个数相加等于target,返回下标。 思路分析 两个方法,不同的时间复杂度 方法一:暴力写法。 复杂度 时间:O(*n*2) 空间:O(1) 123456class Solution: def twoSum(self, nums: List[int], target: int) -> List[int]: for i, x in enumerate(nums): for j in range(i + 1, len(nums)): if...