哈希表
哈希表概述
哈希表:又称散列表,一种以关键码的值「key-value」而直接进行访问的数据结构。任意的键值 key 都唯一对应到内存中的某个位置。只需要输入查找的键值,就可以快速地找到其对应的 value。
哈希函数:根据键值计算索引的函数就叫做哈希函数。
冲突:不同的关键码映射到同一散列位置。key1!=key2,但是H(key1)=H(key2)。
同义词:具有相同函数值的多个关键字。
All in all: 将元素通过一个函数转换为整数,使得该整数可以尽量唯一地代表这个元素 。
需要解决的问题:1. 哈希函数的构造。 2. 冲突解决的方法。
哈希函数构造方法
哈希函数应当易于计算,并且尽量使计算出来的索引均匀分布,以避免冲突。
直接定址法
概述:直接取关键字的某个线性函数值为哈希函数。
哈希函数:H(key) = key 或 H(key) = a*key + b ( a和b为常数 )
特点:计算简单,不会产生冲突,适合关键字分布连续的情况(若不连续,则存储空间浪费很多,空间效率低)。
除留余数法
概述:指把key除以一个数mod得到的余数作为hash值的方法。当mod是一个质数时,H(key)能尽可能均匀覆盖每一个数。所以取mod为不大于表长Tsize但接近或等于表长的质数,即mod<=Tsize且为质数。
哈希函数:H(key) = key % mod
特点:比较常用,关键在mod的选择,如何使得每个关键字通过该函数转换后等概率映射到散列空间的任一地址。
平方取中法
概述:指取key的平方的中间若干位作为hash值的方法,不常用。
特点:适合于关键字的每位取值都不够均匀或均小于散列地址所需位数。
处理冲突的方法
开放定址法(开地址法)
基本思想:有冲突时就去寻找下一个空的散列地址,只要散列表足够大,空的散列地址总能找到,并将数据元素存入。Hi = (H(key) + di) % Tsize (di为增量序列) 计算新的哈希值。
线性探查法
di = 0, 1, 2, … , Tsize-1
发生冲突时,顺序表查看表中下一个元素,直到有空闲单元。会出现聚集现象,降低查询效率。
平方探查法
di = 0² , +1² , -1² , +2² , -2² , … , +k² , -k²
不会出现聚集现象,不能探测所有单元,但至少能探测一半
伪随机探测法
di = 伪随机数序列
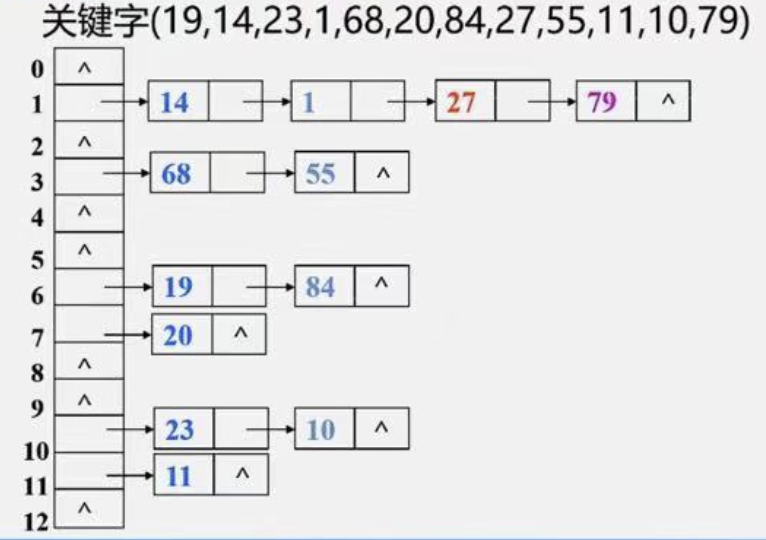
链地址法(拉链法)
基本思想:和上边方法不同,链地址法不计算新的哈希值,而是把相同散列地址的记录链成一单链表。m个散列地址就设m个单链表,然后用一个数组将m个单链表的表头指针存储起来,形成一个动态的结构。
优点:1. 非同义词不会冲突,无”聚集”现象。
2. 链表上结点空间动态申请,更适合于表长不确定的情况(经常插入删除)。
哈希的查找及性能分析
查找过程
检测由散列函数形成的地址上是否有记录,若无记录则失败; 若有记录比较关键字值,若相等则查找成功,否则散列函数更新增量值,重复执行。
性能分析
在列表查找中,使用最广泛的二分查找算法,复杂度为O(log2n),但其始终只能用于有序列表。普通无序列表只能采用遍历查找,复杂度为O(n)。而拥有较为理想的哈希函数实现的哈希表,对其任意元素的查找速度始终为常数级,即O(1)。 链地址法优于开放定址法,除留余数法作散列函数优于其它类型函数。
装填因子:∂=表中记录数/散列表长度。平均查找长度直接依赖于装填因子大小。也就是说,装填因子大小会直接影响到查找效率。装填因子越大,发生冲突的可能性越大。
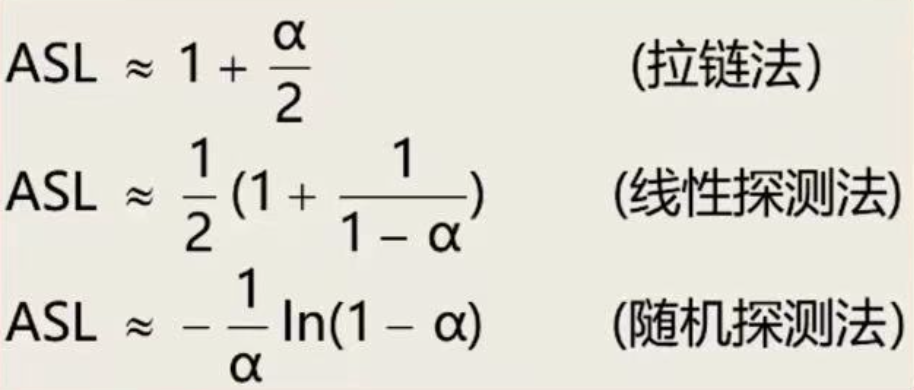
查找效率三个因素影响:哈希函数、装填因子、处理冲突方法。



