图论
图论是数学的一个分支,以图为研究对象。 图论中的“图”是一种抽象的数学结构,由顶点(点)和连接顶点的边(线)构成,用于描述事物之间特定的关系。
- 核心思想: 用点代表事物,用连接两点的线表示事物之间的关系。
[Image of Example Graph with Vertices and Edges]
图的例子:顶点和边
图的基本概念
图 (Graph)
一个图 G 由两个基本集合构成:
- 顶点集 (Vertex Set) V(G): 图中所有顶点的集合。 顶点通常用点、小圆圈或标签表示。
- 边集 (Edge Set) E(G): 图中所有边的集合。 边连接一对顶点,表示顶点之间的关系。 边通常用线段、曲线或箭头表示。
我们可以用数学符号表示一个图: G = (V, E)
顶点 (Vertex / Node / Point)
- 图的基本组成部分,代表研究对象或实体。
- 示例:
- 在社交网络中,顶点可以代表 人。
- 在交通网络中,顶点可以代表 城市。
- 在电路图中,顶点可以代表 电子元件。
边 (Edge / Arc / Line)
- 连接两个顶点的线,表示顶点之间存在的关系。
- 示例:
- 在社交网络中,边可以表示两个人之间的 朋友关系。
- 在交通网络中,边可以表示两个城市之间的 道路。
- 在电路图中,边可以代表 导线。
关联 (Incidence)
- 如果一条边 e 连接了顶点 u 和 v,则称边 e 与顶点 u 和 v 关联。
- 简单来说,就是边“连接到”哪些顶点。
邻接 (Adjacency)
- 顶点邻接: 如果两个顶点 u 和 v 被一条边直接连接,则称顶点 u 和 v 是邻接的。
- 边邻接: 如果两条边 共享 一个公共顶点,则称这两条边是邻接的。
度 (Degree)
一个顶点的度是指与该顶点关联的边的数量。 度反映了顶点与其他顶点的连接数量。
有向图的度: 对于有向图,度分为两种:
- 入度 (In-degree): 指向该顶点的边的数量 (有多少边进入该顶点)。
- 出度 (Out-degree): 从该顶点出发的边的数量 (有多少边从该顶点出发)。
路径 (Path)
- 图中从一个顶点到另一个顶点,依次经过的顶点和边的序列。
- 路径中通常不重复经过顶点,除非是环路。
环路/回路 (Cycle)
- 一种特殊的路径,起点和终点是同一个顶点。
- 环路表示从一个点出发,可以回到原点的路径。
简单路径 (Simple Path)
- 路径中所有顶点都不同的路径。
- 简单路径避免了在路径中重复访问同一个顶点。
简单环路/简单回路 (Simple Cycle)
- 环路中,除了起点和终点相同外,所有其他顶点都不同的环路。
- 简单环路是最基本的环路形式,避免了在环路中重复访问除起点/终点之外的顶点。
图的类型
有向图 vs 无向图
无向图: 边 没有方向,表示连接的两个顶点是互通的。 通常用 (v, w) 表示顶点 v 和 w 之间的无向边。
有向图: 边 有方向,表示连接的两个顶点之间是单向关系。 通常用 <v, w> 表示从顶点 v 指向顶点 w 的有向边。
有权图 vs 无权图
有权图: 图的每条边都被赋予一个 **权重 (weight)**,通常是一个数字。 权重可以代表 距离、成本、时间 等实际含义。
无权图: 图的边 没有权重。 可以理解为所有边的权重都相同(例如权重为 1)。
连通图 vs 非连通图
连通图 (针对无向图): 图中 任意两个顶点之间都存在路径。 这意味着从图中任何一个顶点出发,都可以到达其他任何顶点。
非连通图 (针对无向图): 图中 至少存在一对顶点之间没有路径。 非连通图由多个互相独立的“部分”组成。
连通分量 (Connected Component): 非连通图可以被划分成多个 连通的子图,每个这样的连通子图被称为一个 连通分量。 连通图自身只有一个连通分量,就是它本身。
强连通 vs 单连通
- 强连通 (Strongly Connected): 有向图 中,任意两个顶点之间都存在互相可达的路径。 即从顶点 u 可以到达 v,同时从顶点 v 也可以到达 u。
- 单连通 (Unilaterally Connected): 有向图 中,任意两个顶点之间都存在至少一个方向可达的路径 (无需互相可达)。 即对于任意两个顶点 u 和 v,要么从 u 可以到达 v,要么从 v 可以到达 u,或者两者都成立。
图的表示方法
邻接矩阵表示法
邻接矩阵是一个二维数组,用于表示顶点之间的连接关系:
- 对于无权图,矩阵元素 A[i][j] = 1 表示顶点 i 和 j 之间有边相连,A[i][j]= 0 表示没有边相连
- 对于有权图,矩阵元素 A[i][j]表示顶点 i 和 j 之间边的权值,通常用一个特殊值(如∞或0)表示不存在的边
优点:
- 实现简单,便于理解
- 查询两点间是否有边的时间复杂度为 O(1)
- 适合表示稠密图
缺点:
- 空间复杂度为 O(V²),其中 V 是顶点数,对于稀疏图会浪费大量空间
- 添加/删除顶点的操作较为复杂
邻接表表示法
邻接表使用一个数组,数组的每个元素是一个链表,用于存储与该顶点相邻的所有顶点:
- 数组索引 i 对应顶点 i
- 链表中存储的是与顶点 i 相邻的所有顶点
优点:
- 节省空间,特别适合稀疏图
- 容易找到给定顶点的所有邻接点
- 添加顶点操作简单
缺点:
- 查询两点间是否有边的时间复杂度为 O(V),不如邻接矩阵高效
- 对有向图求逆邻接表较困难
十字链表表示法
十字链表是邻接表的改进版本,主要用于有向图:
- 结合了邻接表和逆邻接表的特点
- 每个顶点有一个出边表和一个入边表
- 每条边用一个结点表示,同时出现在起点的出边表和终点的入边表中
优点:
- 容易找到顶点的所有出边和入边
- 适合需要频繁查询入度和出度的应用场景
邻接多重表
邻接多重表主要用于无向图:
- 每条边只存储一次
- 每个顶点有一个边表
- 每条边连接到与其关联的两个顶点的边表中
优点:
- 便于删除和查找特定边
- 节省空间
边集数组表示法
边集数组直接存储图中所有的边:
- 使用一个一维数组存储所有顶点信息
- 使用另一个数组存储所有边的信息(包括起点、终点和权值)
优点:
- 实现简单
- 适合只关注边的操作,如最小生成树的Kruskal算法
- 适合稀疏图
缺点:
- 查找操作效率较低
- 不易找到与特定顶点相连的所有边
选择哪种表示方法取决于图的特性(如稠密度)和需要执行的操作类型(如是否需要频繁查询、添加或删除顶点和边)。
图的遍历方法
DFS(深度优先搜索)
深度优先搜索沿着图的深度尽可能远地探索,直到不能再深入为止,然后回溯到前一个节点,继续探索其他路径。
基本算法步骤
- 选择一个起始顶点,将其标记为已访问
- 对该顶点的每个未访问的邻接点,递归地应用DFS
- 如果当前顶点没有未访问的邻接点,则回溯
时间复杂度与空间复杂度
- 时间复杂度:O(V + E)
- 空间复杂度:O(V)
应用场景
- 拓扑排序
- 寻找连通分量
- 判断图中是否有环
- 寻找路径(如迷宫问题)
BFS(广度优先搜索)
广度优先搜索是一种按”层次”访问节点的方法,先访问起始顶点的所有邻接点,然后再访问这些邻接点的邻接点,以此类推。
基本算法步骤
- 选择一个起始顶点,将其标记为已访问,并放入队列中
- 当队列不为空时,执行以下操作:
- 取出队列中的第一个顶点u
- 访问顶点u
- 将u的所有未访问过的邻接点标记为已访问并加入队列
时间复杂度与空间复杂度
- 时间复杂度:O(V + E),其中V是顶点数,E是边数
- 空间复杂度:O(V),用于存储访问状态和队列
应用场景
- 寻找最短路径(无权图)
- 网络爬虫
- 社交网络中的关系距离(如”六度分隔”理论)
- 层次遍历
图的应用
最小生成树算法
无向图 G 的生成树是具有 G 的全部顶点,但边数最少的连通子图(连通子图并非连通分量)。一个图的生成树可能有多个。
Kruskal算法
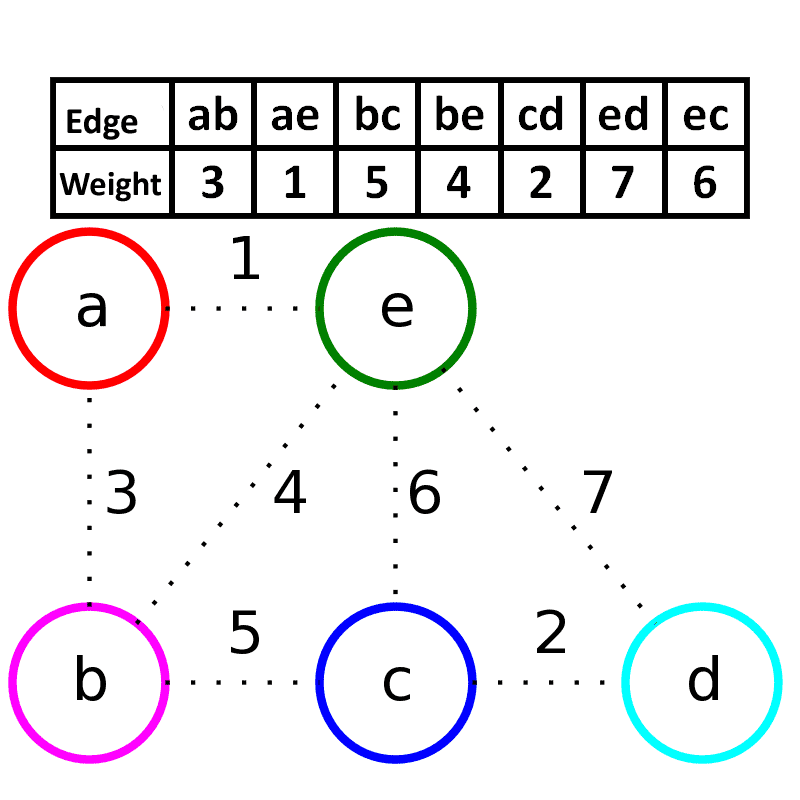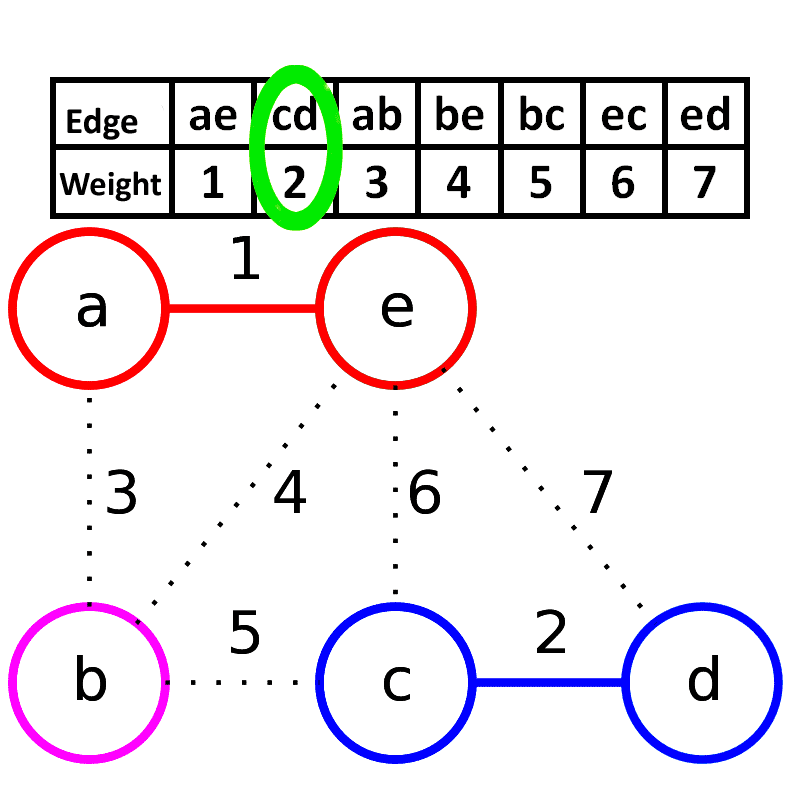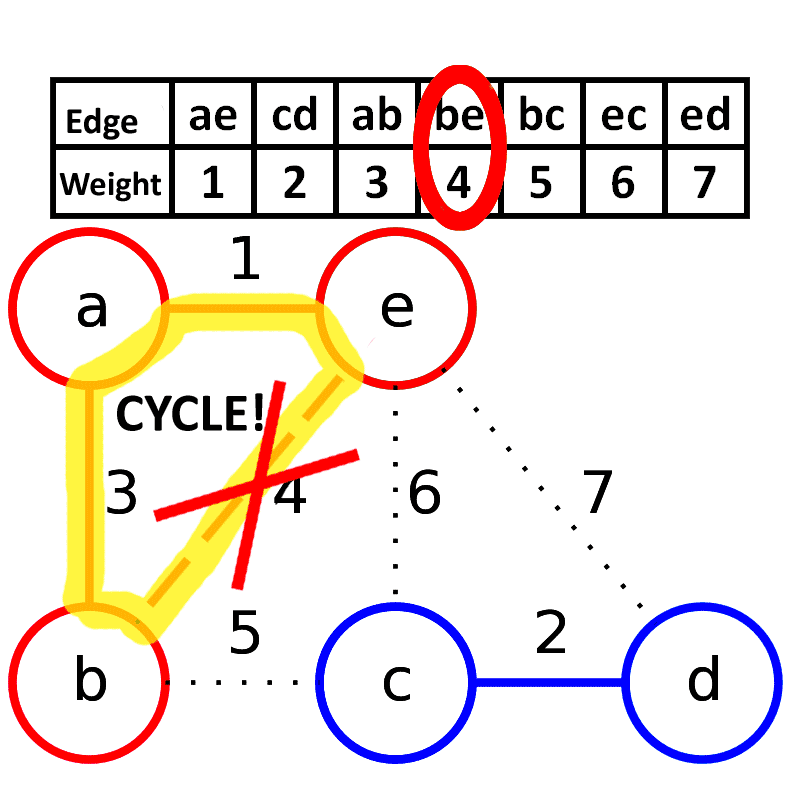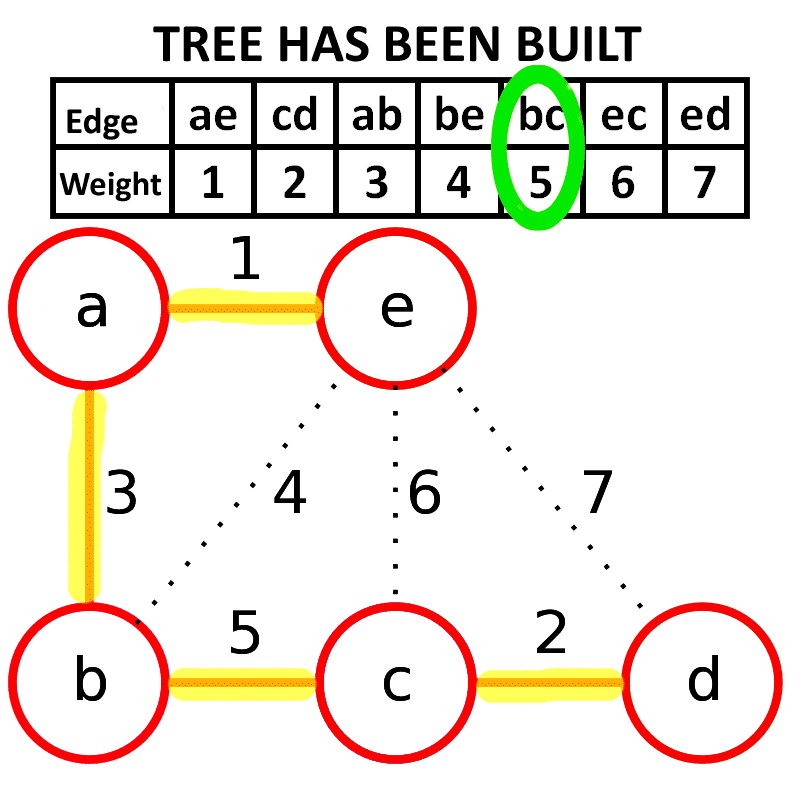
- 思想:贪心策略,每次选择图中权值最小的边,加入生成树中(前提是不形成环)。
- 步骤:
- 对所有边按照权值进行排序。
- 依次从小到大考虑每条边,如果当前边加入后不构成环,则加入生成树。
- 重复直到生成树中包含 n−1 条边。
- 特点:适合边比较少的稀疏图,利用并查集来判断是否形成环。
Prim算法
- 思想:贪心策略,从一个起始顶点开始,每次选择与当前生成树相连的、权值最小的边,将新的顶点加入生成树。
- 步骤:
- 从任一顶点开始,将其加入生成树。
- 找出所有与当前生成树相连的边,选择其中权值最小的边,将边的另一端顶点加入生成树。
- 重复直到所有顶点都被加入生成树。
- 特点:适合边较多的稠密图,通过优先队列(堆)优化可以达到较高效率。
最短路径算法
Dijkstra算法
从起点开始,每次选择当前已知最短距离的顶点,然后更新与它相邻的顶点的距离。
基本流程
- 初始化:源点距离设为0,其他顶点距离设为无穷大
- 每次选择未访问的距离最小的顶点,标记为已访问
- 更新该顶点的邻居顶点的距离
- 重复步骤2-3直到所有顶点被访问
算法复杂度
- 时间复杂度:O(V²),其中V是顶点数。如果使用优先队列优化,可以降低到O((V+E)logV),其中E是边数。
- 空间复杂度:O(V)
算法的局限性
- 迪杰斯特拉算法不能处理负权边
- 在稠密图中,性能可能不如其他算法(如贝尔曼-福特算法)
应用场景
- 导航系统
- 网络路由协议
- 社交网络分析
- 电信网络规划
Floyd-Warshall算法
对于两个顶点i和j之间的最短路径,考虑是否存在一个中间顶点k,使得从i到k再到j的路径比直接从i到j的路径更短。算法通过三重循环遍历所有可能的中间顶点,不断更新距离矩阵。
基本流程
- 初始化一个距离矩阵,矩阵中元素dist[i][j]表示从顶点i到j的直接距离。如果i和j之间没有直接连接,则设为无穷大
- 对于每一个顶点k,检查所有顶点对(i,j)
- 对于每一个顶点对(i,j),如果dist[i][k] + dist[k][j] < dist[i][j],则更新dist[i][j]的值
- 重复步骤2和3,直到遍历完所有顶点
算法复杂度
- 时间复杂度:O(V³),其中V是顶点数
- 空间复杂度:O(V²)
与迪杰斯特拉算法的比较
- 范围不同:迪杰斯特拉是单源最短路径算法,而弗洛伊德是全源最短路径算法
- 适用场景:
- 对于稀疏图,运行V次迪杰斯特拉算法更高效
- 对于稠密图,弗洛伊德算法更优
- 负权边处理:弗洛伊德可以处理负权边,但两者都不能处理负权环
算法优势
- 实现简单,代码简洁
- 可以处理有向图和负权边(但不能有负权环)
- 一次运行可以得到所有顶点对之间的最短路径
应用场景
- 网络路由算法
- 交通规划
- 寻找图中的传递闭包
- 计算最大流问题
A*算法
A*算法是一种启发式搜索算法,常用于路径规划问题。
- 结合了Dijkstra算法和启发式搜索的优点
- 使用估价函数指导搜索方向
- 在有好的启发函数时效率很高
基本流程
- 初始化:起点放入开放列表
- 每次从开放列表中选择f值最小的节点n
- 如果n是目标节点,算法结束
- 否则,将n移到关闭列表,并检查所有邻居节点
- 对于每个邻居,计算经过n的路径长度g和估计总长度f=g+h
- 更新邻居节点信息并加入开放列表
- 重复步骤2-6直到找到目标或开放列表为空
拓扑排序
拓扑排序是一种对有向无环图 (DAG, Directed Acyclic Graph) 中顶点进行线性排序的算法,使得对于图中的每一条有向边 (u, v),顶点 u 在排序中都出现在顶点 v 之前。拓扑排序常用于表示具有依赖关系的任务调度问题。
算法原理
每次选择入度为0的顶点(即没有前驱顶点的顶点),将其输出,然后删除该顶点及其所有出边,重复此过程直到图为空或无法找到入度为0的顶点。
时间复杂度与空间复杂度
- 时间复杂度: O(V + E),其中V是顶点数,E是边数
- 空间复杂度: O(V),需要存储顶点的访问状态和结果
特性和局限性
- 唯一性: 拓扑排序的结果通常不唯一,可能有多种合法的排序方式
- 环检测: 如果图中存在环,则无法进行拓扑排序
- 适用范围: 只适用于有向无环图(DAG)
- 初始点要求: 至少有一个顶点的入度为0,否则无法开始排序


